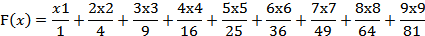第四章
《連續性與可微性的區別》

黎曼清楚的區分了“連續性與可微性之間的差異：在他的論文《用三角級數來表示函數的可表示性》中，黎曼定義了,實際上X是在邏輯上自身之合，於是 (中國數學上的一之一) Ϝ(x) 定義爲


這個級數對所有X值收斂，然而（對于任意的自然數N） , 其中P是一個與2N互質的整數，F(x)是間斷的而且具有一個數值爲 的跳躍。

在X的所有其他數值處，
F(x)是連續的，而且在每個任意小區間上F(x)有無窮多個間斷點。儘管如此，F(x)卻是可積的。而且， 對一切X連續。但是，在 F(x) 的間斷點沒有導數。

黎曼的這個分析例子，在中國原始邏輯圖上可以直接表達兩個九九歌展示的“平方”數概念，什麽是平方數呢？
實際上在原始邏輯的這裏，平方數是非常特殊的，它代表了邏輯本質：自身與自身的合。進一步說，當自然數有序地在一個邏輯正方中出現的時候，唯有正方形的對角線，也就是人們稱為的平方根上的數位置，只有這條線上的自然數才是真正的“平方數”。

它還有另外一個重要數學概念“中心數”,這是一個與平方數關係最為密切,用來構造和表現五行學說的基礎概念。對平方數這個基本概念的把握,人們還需要通過大量的數學演練和邏輯思考,“慢慢地消化”,這個思考很基本,人們會生出“綱舉目張”的釋然!

在一個邏輯正方之中，顯示出自然數的原根是這個自然數本身。“一”這個數本身也自然分爲“陰陽”。平方數的幾何結構是相等相似的，對等性相似性中其符號相反，如同形影：各自互爲對方的有無，表現在自然數上即有顯有隱。八十一個自然數在邏輯正方中，被“陰陽”割列爲一陰一陽，形成兩個九九八十一直角三角形。上述式子中的平方數則形成了一陰一陽之間的“公共邊”“交合綫”，故《周髀算經》曰，“合矩以爲方”。



圖示可見：，邏輯指出唯有自身之和才能表達“平方”數的概念。因而在第一個九九八十一邏輯上的是這樣一組自然數：1，11，21，31，41，51，61，71，81。
繼續排下來，可列出不同性質的秩序圖：顯示F(x)是間斷的而且具有一個數值爲 的跳躍這樣一個邏輯與自然共有的本質性質及其規律。


邏輯所揭示的規律在數學的演繹中意義重大。數是相等的。發現連續性幷不包含可微性，以及函數可以具有的非同一般的同構與自相似性質，我認爲其意義在於：他們提示數學家們更不能簡單的相信直觀要對幾何上“不可共度”綫的進行更爲深刻的思考了。
上一页下一页