數之法 什麽是數?
引子:數之法提出的思考
組成“數”的斷符元素從何而來?
從不可數到可數
從八十一方圖開始幷結束
原来如此!九九歌就是邏輯的數語
数学如何发展了逻辑?
邏輯“分合”形數
九九八十一方圖的邏輯依據
關於“一”的非語言形式
老子是最偉大的數學家
等級與次序即“數自身”
秩序即“數自身”事實始終的統一
如何看待傳統的三段論邏輯
元邏輯與素數的關係
自然结构与逻辑关系构造出来
自身獨存性的理性意義
《平方數,黃金分割與三角形數》
 這裡每一行的點數其實就是自然數與三角形數 1+2+3+4+5+6+7+8+9+10。。。 ∆_n≡1,3,6,10,15,21,28,36,45,55。。。 真好玩,看了沒有?自然數規規矩矩地“藏”在兩個三角形的縫隙裏!
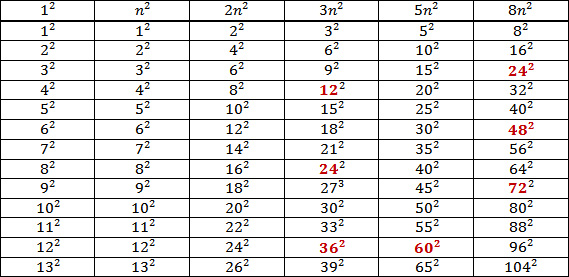
因此,可以用兩個三角形數直观平方數“先天后天”的自合概念的自然特徵。平方數的內在邏輯結構可以寫成先後兩個三角形數的和。
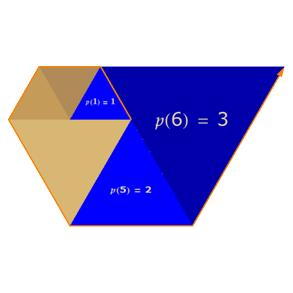
還有一個類似的優美證明,模仿《周髀算經》數之法用勾股定理完成的。 運用圓規直尺和幾何學的勾股定理,我們將黃金分割“馬走日”,作黃金分割矩形的邏輯起點作圖,平面圖顯示出中國黃金分割是使用平方概念排列黃金矩形,每一個黃金矩形均有六個“原根”。 組成,它們之間完全可以用整數替代表達與自然數同樣的邏輯秩序,形成如下結構關係。

這樣的結構,使得自然數之間形成了一定的幾何關係式,這種完全內在的自身性質 的數理關係保證了數具備了個體概念沒有大小多少內涵外延上的限制的單純特徵, 即一性,因此一性就是自然數的天性。
上面的結構關係在直觀上好像是愈來愈趨向“微”,實際上,正如老子描繪的“大曰逝,逝曰遠,遠曰返”向自身递归。。。我想,上面的“數學”原則也可以用來支援柏拉圖的“理念世界”。 世界的實體和大象只能规定一种至簡形式,不能规定任何物质的属性,這就是無實形體系。自然之存在“物”並非一定確知實體,它的“一物兩體”的虛無概念,在數學這裡得到了清新簡明的概括和劃分。
The Fibonacci numbers for n = 1, 2, ... are 1, 1, 2, 3, 5, 8, 13, 21, ...
|
| 上一页 | 下一页 |

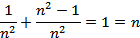
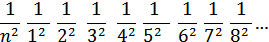

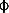 (n)=
(n)=