《學題七》

通天连列图





此为最大尺寸。在數學中，特別是實分析，利普希茨條件（Lipschitz condition）限制了函數改變的速度。符合利普希茨條件的函數的斜率，必小於一個稱為利普希茨常數的實數（該常數依函數而定）。
在微分方程，利普希茨條件確保了初值問題存在唯一解。（详见后面章节Picard-Lindelöf定理）
它以魯道夫•利普希茨命名。

"For a Lipschitz continuous function, there is a double cone (shown in white) whose vertex can be translated along the graph, so that the graph always stays entirely outside the cone."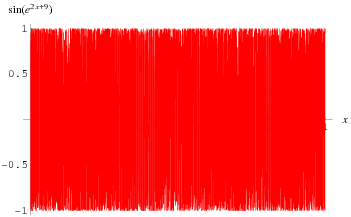


Another pathological example is 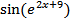near 0 and 1, which has 這裡是不是很酷似夏至狀態的 黃道 數據近似黃金分割，而和日矩



日矩extrema in the closed interval [0,1] (Mulcahy 1996).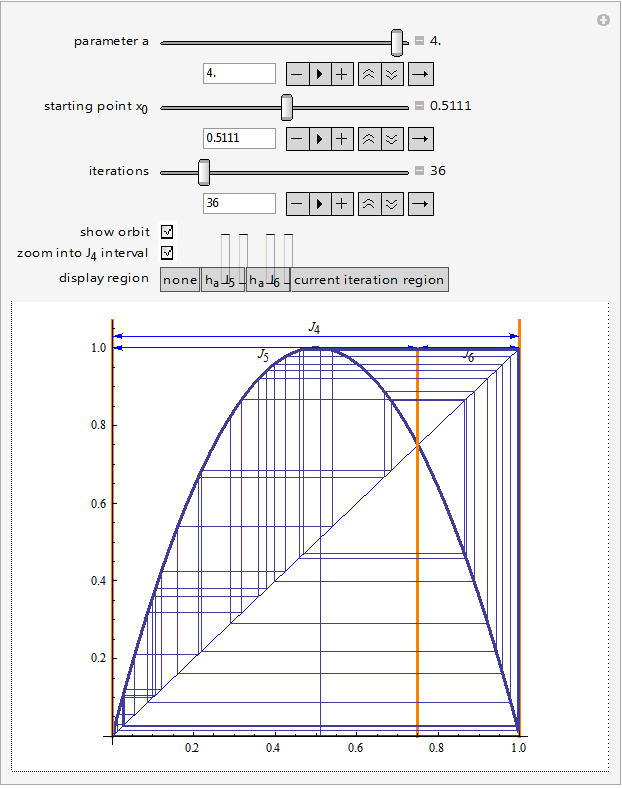




This Demonstration considers the iterations of the logistic map ha(x)=ax(1-x) for 3 ≤ a ≤ 4.
The Demonstration "An Interval Eventually Bounding Trajectories of the Logistic Map" showed how every trajectory with a starting point in (0, 1) is eventually contained in J4=[ha(a/4),a/4]. This Demonstration shows that there cannot be any odd periodic orbit if
a ≤ ad=3/2 (1+(19+3)1/3+(19-3)1/3)≈3.67857.

In fact, in that case the interval J5=(ha(a/4),(a-1)/a) is mapped into the interval J6=((a-1)/a,a/4) and J6 is mapped into J5. It is also easy to show that the points ha(a/4),(a-1)/a, and a/4 do not lead to an odd periodic orbit. The previous statements are not true if ad ≤ a ≤ 4.