《勾股定理的73種證明》

Proof #1

This is probably the most famous of all proofs of the Pythagorean proposition. It's the first of Euclid's two proofs (I.47). The underlying configuration became known under a variety of names, the Bride's Chair likely being the most popular.


The proof has been illustrated by an award winning Java applet written by Jim Morey. I include it on a separate page with Jim's kind permission. The proof below is a somewhat shortened version of the original Euclidean proof as it appears in Sir Thomas Heath's translation.

First of all, ΔABF = ΔAEC by SAS. This is because, AE = AB, AF = AC, and

BAF = BAC + CAF = CAB + BAE = CAE.

ΔABF has base AF and the altitude from B equal to AC. Its area therefore equals half that of square on the side AC. On the other hand, ΔAEC has AE and the altitude from C equal to AM, where M is the point of intersection of AB with the line CL parallel to AE. Thus the area of ΔAEC equals half that of the rectangle AELM. Which says that the area AC2 of the square on side AC equals the area of the rectangle AELM.

Similarly, the are BC2 of the square on side BC equals that of rectangle BMLD. Finally, the two rectangles AELM and BMLD make up the square on the hypotenuse AB.

The configuration at hand admits numerous variations. B. F. Yanney and J. A. Calderhead (Am Math Monthly, v.4, n 6/7, (1987), 168-170 published several proofs based on the following diagrams



Proof #2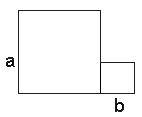

         
We start with two squares with sides a and b, respectively, placed side by side. The total area of the two squares is a2+b2.

The construction did not start with a triangle but now we draw two of them, both with sides a and b and hypotenuse c. Note that the segment common to the two squares has been removed. At this point we therefore have two triangles and a strange looking shape.


As a last step, we rotate the triangles 90°, each around its top vertex. The right one is rotated clockwise whereas the left triangle is rotated counterclockwise. Obviously the resulting shape is a square with the side c and area c2. This proof appears in a dynamic incarnation.

(A variant of this proof is found in an extant manuscript by Thâbit ibn Qurra located in the library of Aya Sofya Musium in Turkey, registered under the number 4832. [R. Shloming, Thâbit ibn Qurra and the Pythagorean Theorem, Mathematics Teacher 63 (Oct., 1970), 519-528]. ibn Qurra's diagram is similar to that in a proof #27. The proof itself starts with noting the presence of four equal right triangles surrounding a strangely looking shape as in the current proof #2. These four triangles correspond in pairs to the starting and ending positions of the rotated triangles in the current proof. This same configuration could be observed in a proof by tessellation.)

Source: http://www.cut-the-knot.org/pythagoras/index.shtml