《勾股定理的N種證明3-6》

Proof #3

          

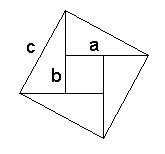Now we start with four copies of the same triangle. Three of these have been rotated 90o, 180o, and 270o, respectively. Each has area ab/2. Let's put them together without additional rotations so that they form a square with side c.

The square has a square hole with the side (a - b). Summing up its area (a - b)2 and 2ab, the area of the four triangles (4•ab/2), we get

c2 = (a - b)2 + 2ab = a2 - 2ab + b2 + 2ab = a2 + b2


Proof #4

The fourth approach starts with the same four triangles, except that, this time, they combine to form a square with the side (a + b) and a hole with the side c. We can compute the area of the big square in two ways. Thus

(a + b)2 = 4•ab/2 + c2

simplifying which we get the needed identity.
A proof wich combines this with proof #3 is credited to the 12th century Hindu mathematician Bhaskara (Bhaskara II):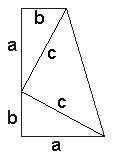
                         

Here we add the two identities  c2 = (a - b)2 + 4•ab/2 and c2 = (a + b)2 - 4•ab/2

which gives
2c2 = 2a2 + 2b2.
The latter needs only be divided by 2. This is the algebraic proof # 36 in Loomis' collection. Its variant, specifically applied to the 3-4-5 triangle, has featured in the Chinese classic Chou Pei Suan Ching
《周髀算经》 dated somewhere between 300 BC and 200 AD and which Loomis refers to as proof 253.


Proof #5

This proof, discovered by President J.A. Garfield in 1876 [Pappas], is a variation on the previous one. But this time we draw no squares at all. The key now is the formula for the area of a trapezoid - half sum of the bases times the altitude - (a + b)/2•(a + b). Looking at the picture another way, this also can be computed as the sum of areas of the three triangles - ab/2 + ab/2 + c•c/2. As before, simplifications yield a2 + b2 = c2.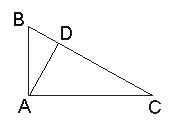
                   
Two copies of the same trapezoid can be combined in two ways by attaching them along the slanted side of the trapezoid. One leads to the proof #4, the other to proof #52.

Proof #6

We start with the original triangle, now denoted ABC, and need only one additional construct - the altitude AD. The triangles ABC, BDA and ADC are similar which leads to two ratios:
AB/BC = BD/AB and AC/BC = DC/AC. 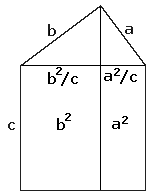            Summing up we get

AB•AB + AC•AC = BD•BC + DC•BC = (BD+DC)•BC = BC•BC.

In a little different form, this proof appeared in the Mathematics Magazine, 33 (March, 1950), p. 210, in the Mathematical Quickies section, see Mathematical Quickies, by C. W. Trigg.
Taking AB = a, AC = b, BC = c and denoting BD = x, we obtain as above

a2 = cx and b2 = c(c - x), 

which perhaps more transparently leads to the same identity.
In a private correspondence, Dr. France Dacar, Ljubljana, Slovenia, has suggested that the diagram on the right may serve two purposes. First, it gives an additional graphical representation to the present proof #6. In addition, it highlights the relation of the latter to proof #1.

It must be mentioned that this proof is just a variant of the next one - Euclid's second and less known proof of the Pythagorean proposition.

Source: http://www.cut-the-knot.org/pythagoras/index.shtml